ml - Introduzione interattiva di MATLAB       Vai all'indice del corso

Grafici di funzioni di variabile reale
Versione 0.7

Indice del modulo

2gfr.00 - Grafici di funzioni di variabile reale
2gfr.10 - Grafici di funzioni lineari
2gfr.11 - Funzioni lineari e sistemi di 2 equazioni lineari
2gfr.14 - Grafici di x^2 e radice quadrata
2gfr.15 - Polinomi ed equazioni di secondo grado
2gfr.17 - Grafici di x^3 e radice cubica
2gfr.18 - Grafici di polinomi cubici
2gfr.20 - Grafici di seno e coseno
2gfr.22 - Grafici di arcoseno ed arcocoseno
2gfr.24 - Grafici di tangente e cotangente
2gfr.25 - Grafici di arcotangente ed arcocotangente
2gfr.26 - Grafici del quadrato, del cubo e della radice del seno
2gfr.27 - Grafici del seno di x^2 e x^3
2gfr.30 - Grafici di seno iperbolico e coseno iperbolico
2gfr.32 - Grafici di tangente iperbolica e secante iperbolica
2gfr.40 - Grafici di funzioni x^n*exp(x)
2gfr.41 - Grafici di funzioni gaussiane
2gfr.42 - Grafici di funzioni gaussiane
2gfr.43 - Grafici di funzioni con exp, log ed abs
2gfr.44 - Grafici di funzioni con logaritmi
2gfr.45 - Grafici di funzioni con sin
2gfr.46 - Grafici di funzione con sin
2gfr.51 - Grafici di funzioni con exp, sin e cos
2gfr.70 - Grafici di funzioni con punti singolari
2gfr.71 - Grafico della funzione sin(1/x)
2gfr.72 - Grafici di funzioni con sin(1/x)
2gfr.75 - Grafico della funzione exp(1/x)

torna all'indice del modulo - del corso

2gfr.00 - Grafici di funzioni di variabile reale

Puo` essere molto utile servirsi di MATLAB per familiarizzarsi con le funzioni di variabile reale, specialmente di quelle elementari che si incontrano piu` spesso in applicazioni significative. In particolare e` utile prendere visione di grafici che consentono di confrontare funzioni diverse servendosi di colori e stili diversi per le loro curve.

Sono utili confronti come i seguenti:
funzioni dipendenti da un parametro relative a suoi diversi valori;
funzioni ottenibili l'una dall'altra mediante trasformazioni significative come traslazioni, riflessioni, dilatazioni, passaggi ai valori reciproci;
funzioni ottenibili con composizioni di funzioni via via piu` complesse.

torna all'indice del modulo - del corso

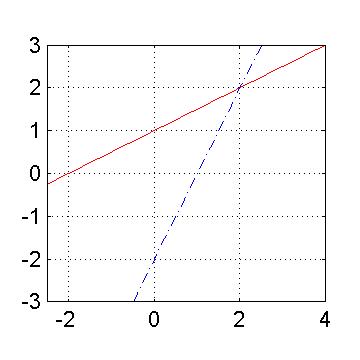
2gfr.10 - Grafici di funzioni lineari

Si osservino i seguenti grafici di linee rette.

>> x1=-2.5:.1:4;
>> y1=1.+.5.*x1;
>> x2=-.5:.1:2.5;
>> y2=-2.+2.*x2;
>> plot(x1,y1,'-r',x2,y2,'-.b')
>> grid on, axis equal tight

Si osservi che le due rette tracciate in rosso e blu sono simmetriche rispetto la bisettrice del primo e del terzo quadrante (y=x). Dato che riflettere rispetto questa bisettrice equivale a scambiare le ascisse con le ordinate, la simmetria rispetto questa riflessione equivale al fatto che le due funzioni sono l'una l'inversa dell'altra. Questo equivale anche al fatto che le relazioni stabilite dalle due assegnazioni

y1=1.+.5.*x1;       y2=-2.+2.*x2;

diventano equivalenti quando si identifichino   x1 con y2   ed   x2 con y1 e si suppone che le variabili assumono tutti i valori reali

torna all'indice del modulo - del corso

2gfr.11 - Funzioni lineari e sistemi di 2 equazioni lineari

Si osservi il seguente grafico delle seguenti funzioni lineari.

>> x=-1:0.05:1;
>> plot(x,arcsin(x),'-r',x,arccos(x),'-.b')
>>

torna all'indice del modulo - del corso

2gfr.14 - Grafici di x^2 e radice quadrata

Si osservino i grafici delle funzioni x^2 e radice quadrata.

>> x=-1:0.05:1;
>> plot(x,arcsin(x),'-r',x,arccos(x),'-.b')
>>

Osserviamo che le due funzioni considerate per x>=0 sono l'una l'inversa dell'altra

torna all'indice del modulo - del corso

2gfr.15 - Polinomi ed equazioni di secondo grado

Si osservino i grafici delle funzioni x^2 e radice quadrata.

>> x=-1:0.05:1;
>> plot(x,arcsin(x),'-r',x,arccos(x),'-.b')
>>

Osserviamo che le due funzioni considerate per x>=0 sono l'una l'inversa dell'altra

torna all'indice del modulo - del corso

2gfr.17 - Grafici di x^3 e radice cubica

Si osservino i grafici delle funzioni seno e coseno.

>> x=-1:0.05:1;
>> plot(x,arcsin(x),'-r',x,arccos(x),'-.b')

torna all'indice del modulo - del corso

2gfr.18 - Grafici di polinomi cubici

Si osservino i grafici delle funzioni seno e coseno.

>> x=-1:0.05:1;
>> plot(x,arcsin(x),'-r',x,arccos(x),'-.b')

torna all'indice del modulo - del corso

2gfr.20 - Grafici di seno e coseno

Si osservino i grafici delle funzioni seno e coseno.

>> x=-3.5:0.05:3.5;
>> plot(x,sin(x),'-r',x,cos(x),'-.b')

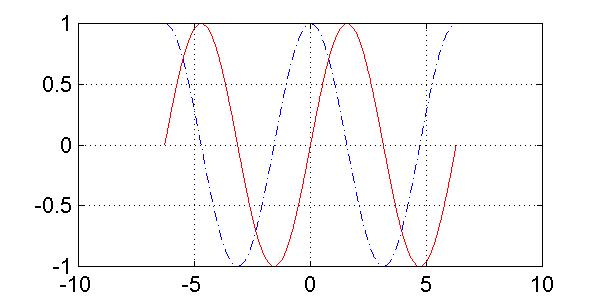
Da essi risultano evidente le periodicita`, la simmetria del coseno, l'antisimmetia del seno e la proprieta` di traslazione sin(x)=cos(x-pi/2).

torna all'indice del modulo - del corso

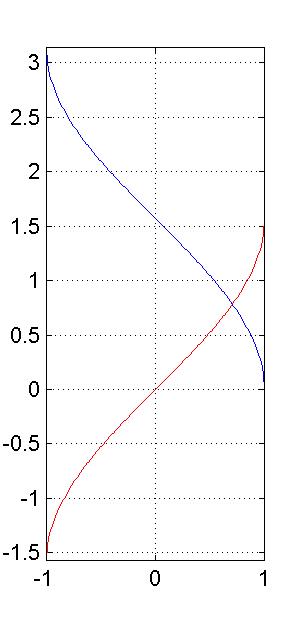
2gfr.22 - Grafici di arcoseno ed arcocoseno

Si osservino i grafici delle funzioni arcoseno ed arcocoseno. 

>> x=-1:0.01:1;
>> plot(x,asin(x),'-r',x,acos(x),'-b')
>> grid on, axis equal tight

torna all'indice del modulo - del corso

2gfr.24 - Grafici di tangente e cotangente

Si osservino i grafici delle funzioni tangente e cotangente

>> x=-1.25*pi:pi/15:1.25*pi;
>> plot(x,tan(x),'-r',x,cotan(x),'-.b')
>>

torna all'indice del modulo - del corso

2gfr.25 - Grafici di arcotangente ed arcocotangente

Si osservino i grafici delle funzioni arcotangente ed arcocotangente. 

>> x=-3:0.1:3;
>> plot(x,atan(x),'-r',x,acotan(x),'-.b')

torna all'indice del modulo - del corso

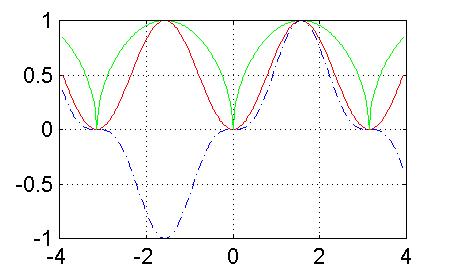
2gfr.26 - Grafici del quadrato, del cubo e della radice del seno

Si osservino i grafici delle seguenti funzioni trigonometriche periodiche.

>> x=-1.25*pi:pi*0.01:1.25*pi;
>> plot(x,sin(x).^2,'-r',x,sin(x).^3,'-b')
>>

torna all'indice del modulo - del corso

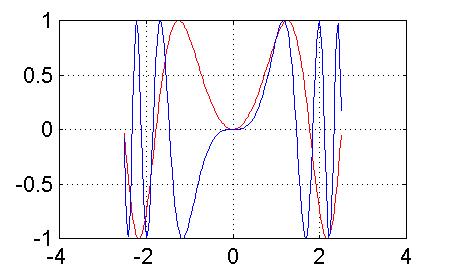
2gfr.27 - Grafici del seno di x^2 e x^3

Si osservino i grafici delle seguenti funzioni trigonometriche non periodiche.

>> x=-2*pi:pi*0.01:2*pi;
>> plot(x,sin(x.^2),'-r',x,sin(x.^3),'-b')
>>

torna all'indice del modulo - del corso

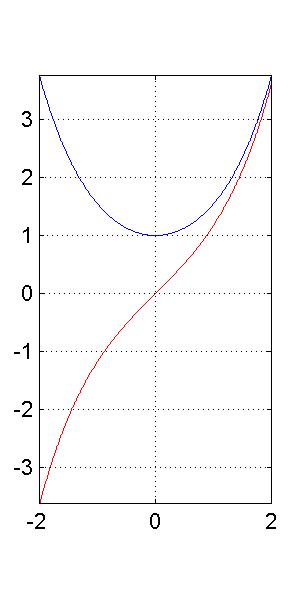
2gfr.30 - Grafici di seno iperbolico e coseno iperbolico

Si osservino i grafici delle funzioni seno iperbolico e coseno iperbolico. 

>> x=-2.:0.01:2.;
>> plot(x,sinh(x),'-r',x,cosh(x),'-.b')
>> grid on, axis equal tight

torna all'indice del modulo - del corso

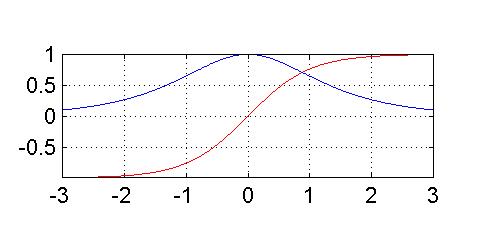
2gfr.32 - Grafici di tangente iperbolica e secante iperbolica

Si osservino i grafici delle funzioni tangente iperbolica sinh(x)/cosh(x) e secante iperbolica 1/cosh(x).

>> x=-2.01:0.02:2.01;
>> plot(x,tanh(x),'-r',x,sech(x),'-.b')
>> grid on, axis equal tight

torna all'indice del modulo - del corso

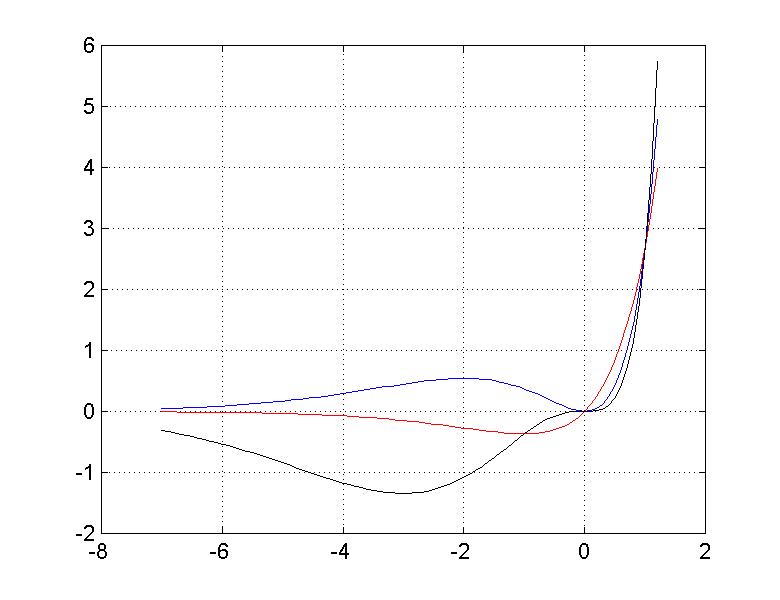
2gfr.40 - Grafici di funzioni x^n*exp(x)

Si osservino i grafici di funzioni reali ottenute con le seguenti frasi. 

>> x=-7:0.10:1.25;
>> plot(x,x*exp(x),'-r',x,x^2*exp(x),'-.b',x,x^3*exp(x),'.g')
>>

torna all'indice del modulo - del corso

2gfr.41 - Grafici di funzioni gaussiane

Si osservino i grafici delle funzioni ottenute con le seguenti frasi. 

>> x=-2.5:0.01:4.5;
>> plot(x,exp(-x.^2),'-r',x,exp((x-1).*(x-2)),'-.b',x,exp((x+.1).*(x-.5)),'-g')
>>

torna all'indice del modulo - del corso

2gfr.42 - Grafici di funzioni gaussiane

Si osservino i grafici di funzioni reali ottenute con le seguenti frasi. 

>> x=-3:0.05:3;
>> plot(x,exp(-1./x.^2),'-r',x,exp(1./(x.^2-1)),'-.b')
>>

torna all'indice del modulo - del corso

2gfr.43 - Grafici di funzioni con exp, log ed abs

Si osservino i grafici di funzioni reali ottenute con le seguenti frasi. 

>> x=-4:0.05:4;
>> plot(x,exp(-abs(x)),'-r',x,log(abs(x1)),'-.b')
>>

torna all'indice del modulo - del corso

2gfr.44 - Grafici di funzioni con logaritmi

Si osservino i grafici di funzioni reali ottenute con le seguenti frasi. 

>> x=0:0.05:2;
>> plot(x,x*log(x),'-r',x,x^2*log(x),'-.b',x,x^x,':g')
>>

torna all'indice del modulo - del corso

2gfr.45 - Grafici di funzioni con sin

Si osservino i grafici di funzioni reali ottenute con le seguenti frasi. 

>> x=-2.25*pi:pi/20:2.25*pi;
>> plot(x,x*sin(x),'-r',x,sin(x)/x,':g')
>>

torna all'indice del modulo - del corso

2gfr.46 - Grafici di funzione con sin

Si osservino i grafici di funzioni reali ottenute con le seguenti frasi. 

>> x=-6/pi:0.1/pi:6/pi;
>> plot(x,sin(1/x),'-r',x,(sin(1/x))^2,':g')
>>

torna all'indice del modulo - del corso

2gfr.51 - Grafici di funzioni con exp, sin e cos

Si osservino i seguenti grafici di funzioni reali ottenute componendo funzioni trascendenti elementari. 

>> x=0:pi/15:4*pi;
>> e2c=exp(2*cos(x));
>> plot(x,e2c,'r+')
>> plot(x,e2c,'+')
>> e2s=exp(2*sin(x));
>> plot(x,e2c,'-*k',x,e2c,'-.ok')
>>

torna all'indice del modulo - del corso

2gfr.70 - Grafici di funzioni con punti singolari

Quando si vogliono grafici di funzione con punti nei quali qualche sottoespressione non e` definita con MATLAB si possono incontrare problemi legati alle approssimazioni numeriche che esso effettua. Bisogna allora procedere con attenzione; spesso e` opportuno procedere per passi successivi chiarendo via via i punti critici dei calcoli che si richiedono: questo puo` effettuarsi sia con studi analitici sulle espressioni da trattare, sia con indagini empiriche effettuate con tentativi via via piu` consapevoli e mirati.

torna all'indice del modulo - del corso

2gfr.71 - Grafico della funzione sin(1/x)

Si voglia il grafico della funzione sin(1/x). Un primo tentativo ingenuo puo` essere il seguente.

>> x=-pi*2:pi/100:pi*2;
>> plot(x,sin(1./x),'-r')
Warning: Divide by zero.
>>
In effetti la sequenza x di valori per la variabile indipendente contiene 0 e per questo valore 1/x non e` calcolabile. Riproviamo con una sequenza x che escluda lo 0; la scelta piu` semplice e` la seguente. 
>> x=-pi*2.005:pi*0.01:pi*2.005;
>> plot(x,sin(1./x),'-r')
>>

La figura ottenuta da una chiara idea dell'andamento della funzione per |x| abbastanza grande, diciamo superiore a 0.5; in vicinanza dell'origine indica solo un andamento oscillante che conviene chiarire con un grafico circoscritto, con una sorta di zoom

>> x=-pi*0.2005:pi*0.001:pi*0.2005;
>> plot(x,sin(1./x),'-r')
>>

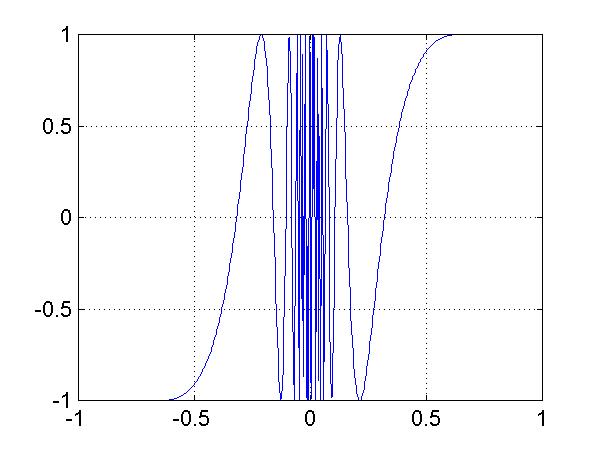
La nuova figura fornisce indicazioni piu` chiare sulle oscillazioni che si addensamento all'avvicinarsi a 0. Si puo` fare un ulteriore raffinamento che prende in considerazione solo valori positivi della variabile, dopo aver constatata la antisimmetria

sin(1/(-x)) = - sin(1/x).

>> x=pi*0.0001:pi*0.0001:pi*0.1;
>> plot(x,sin(1./x),'-r')
>>

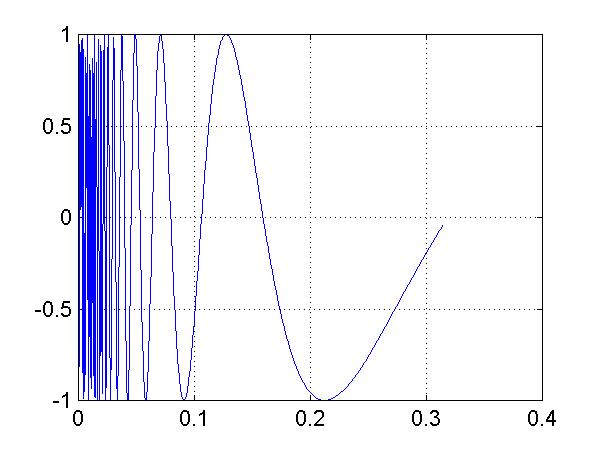
torna all'indice del modulo - del corso

2gfr.72 - Grafici di funzioni con sin(1/x)

Si osservino i grafici delle due funzioni ottenute con le seguenti frasi .

>> x=-pi*0.5025:pi*0.005:pi*0.5025;
>> plot(x,x.*sin(1./x),'-r',x,x.^2.*sin(1./x),'-b')
>>

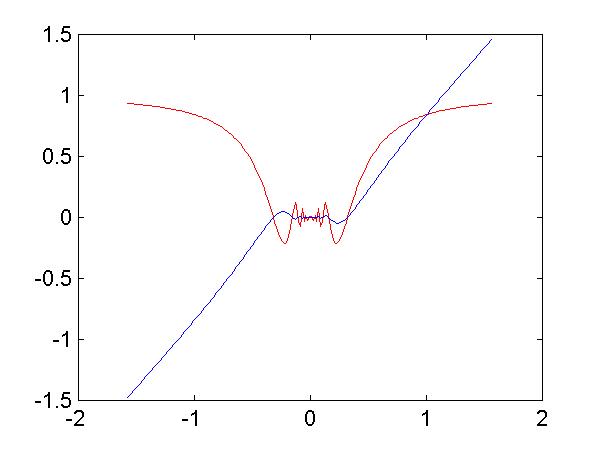
Anche per queste funzioni e` utile uno zoom che si puo` limitare a valori di x positivi. 

>> x=0.0001:0.0001:0.5;
>> plot(x,x.*sin(1./x),'-r',x,x.^2.*sin(1./x),'-b')
>>

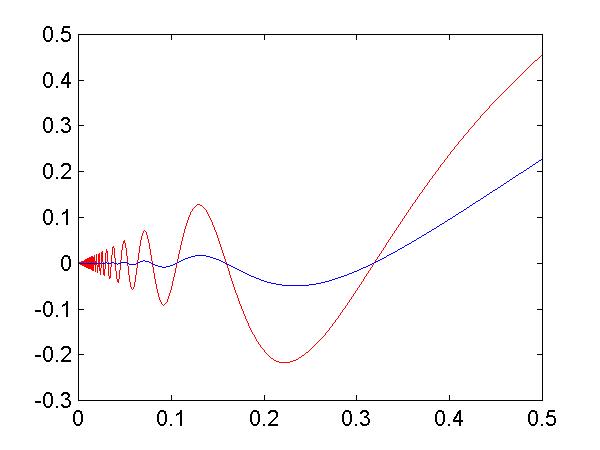
torna all'indice del modulo - del corso

2gfr.75 - Grafico della funzione exp(1/x)

La funzione exp(1/x) non e` definita per x=0; conviene considerare la sequenza dei valori della x divisa in due parti separate.

>> x1=-4:0.01:-0.01; x2=0.6:0.1:4.0;
>> plot(x1,exp(1./x1),'-r',x2,exp(1./x2),'-r')
>>

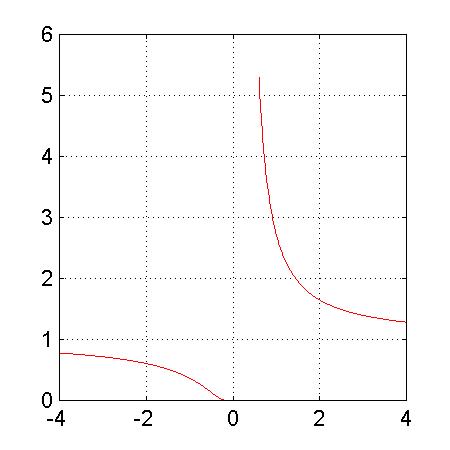
Osserviamo che se si considerano valori di x positivi piu` vicini a 0 di 0.6 si avrebbe un grafico schiacciato sull'esse x a causa dei valori elevati assunti dalla funzione per le suddette x.

torna all'indice del modulo - del corso